放送大学・山口学習センターで「数学の講座」が開設される…という理由だけで参加したのが今回の面接授業でした。
内容のほとんどが命題論理で、大学の数学科では授業の1〜2コマで一気にやられる内容を、2日間の7.5コマを使ってゆっくり説明される講座でした。
命題論理については、大学のみならず予備校でも習った記憶があります。駿台の小林隆章先生(大学への数学)や長岡恭史先生(数学ぐんぐん)、某科学的教育グループの水野谷先生(数学の文法)など。
最近は、論理の内容が掲載されている学習参考書(注)がいっぱいありますね
担当の隈部先生は、その都度・頻繁に質問を受け付ける形で講義を進めていました。
受講生の方も、疑問点は遠慮なく質問していました。「もう一度説明していただけませんか」のような質問もありました。
講義は4つの記号、∧,∨,→,¬の紹介から始まりました。
「A→B(A,B:命題)と(¬A)∨Bが同じ意味(*1)になる(…と隈部先生は説明していました)」
ことは、数学科の1年生で、散々やらされると思いますが、
隈部先生は(*1)から「→(ならば)の記号はなくても、命題は表現できることになりますね」と説明していました。
言われてみれば確かに…何で今まで気づかなかったんでしょうかね…私。
数学科卒のはずなんですが、大学で一体何を勉強してたんでしょう?
ド・モルガンの法則を使えばさらに論理記号を1つ減らせるので、命題は論理記号2つ(例えば、∨と¬)で表現できることになります。
…とは言っても、「明日晴れたらピクニックを行く(明日晴れ→ピクニックに行く)」ことと「『明日晴れない』または『ピクニックに行く』」ことは、論理の上では同じでも、分かりやすさは全く異なるので、(分かりやすさ・便利さのためにも)論理記号は4つを使ったほうがいいですね。
なお、上記は「そのように隈部先生が言っていた・説明していた」ということなので、数学ガチ勢によるガチ勢のツッコミは、私にしないようお願い申し上げます。(あくまで、この文章は講座のレポートです)
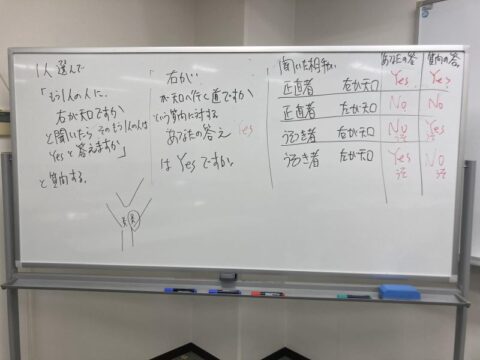
1日目の終わりに宿題があって、見たことがある人なら分かる次の問題が示されました。
ある旅人が一本道を歩いていたところ道が二手に別れていた。そこに二人の老人がいた。
一方は天国に行く道で他方は地獄へ行く道である。
一人はいつも正直な回答(正直者)をし、もう一人はいつも嘘の回答(嘘つき)をする。
どちらが正直者で、どちらが嘘つきかわからないし、どちらも「はい」か「いいえ」しか言わない。
旅人は一人だけ選んで一回だけ質問することができる。天国に行くためにはどのような質問をすればよいか?
引用:『数学基礎論』(隈部正博:著)
よく知られた回答の方針は次の2つで
【回答の方針】
① 嘘つきに2回、嘘を言わせる質問
② どのような場合でも嘘が1回入るようにする質問
回答は
この回答はエレガントですが、それ故、まぁ〜思いつきません。
そのため、この回答は受験数学で言うところの「パターン暗記」に属するモノになります。
「知っていれば解ける、知らないと解けません」と言う類のモノですね。
もちろんこの質問を閃く人もいるんでしょうが、それはごくごく一部の人(数学オリンピックのメダリストなど、0.1% 未満の人)で、初見解くことはほとんどの人が無理でしょう。
あ、なお、私は「パターン暗記」否定派の人間ではありません。大学の数学はご多分に漏れず「パターン暗記」で乗り切った人間です。
また、この回答はネット上探せば至る所で見つかります。
が、肝心の隈部先生の回答は違かったんですね。ちゃんと意味を後付けではなく(上記の解説は後付け。人間の脳は、必然性のない回答を必然性があるように創作するのが得意です。)必然性のある回答を示していました。で、その回答を書くにはスペースが足りないので、後日書きたいと思います。
追伸:帰りの湯田温泉駅でSLやまぐち号に遭遇しました。
注:受験向けは上3つ(1〜3)、一般雑学向けは下3つ(4〜6)
1.数学の真髄 ―論理・写像―
2.総合的研究 論理学で学ぶ数学
3.総合的研究 問題文の読み取り方
4.数学の基礎体力をつけるためのろんりの練習帳
5.ろんりと集合
6.数学教師が教える やさしい論理学