算数教育や数学教育関連の学会に参加すると必ずお見かけする「ぐるぐるの図」について、補足したいと思います。
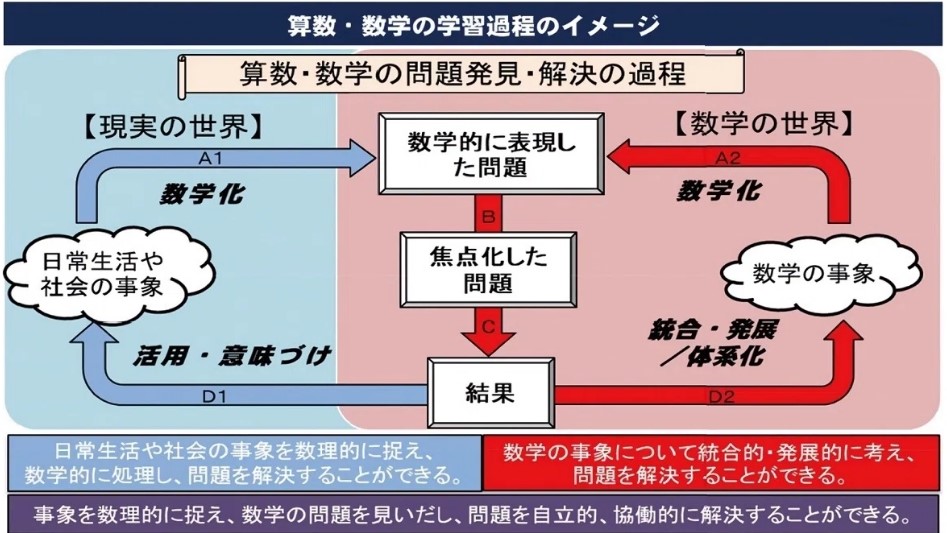
ぐるぐるの図は、次のようなステップがあります。
\(A_1\):日常生活や社会の事象を見つける
まずは身の回りにある「気になること」「解決したい問題」を見つけます。たとえば「旅行の費用を安くするにはどうしたらいいか?」など、リアルな問題が出発点です。
これを「数学的に見立てられそうな要素は何か?」という視点で見るところが重要です。
\(A_2\):数学的に表現する
見つけた事象を、数や式、図、グラフなどの形で“数学に落としこむ”作業です。
たとえば、旅行費用の事例なら「交通費を変数\(x\)、宿泊費を変数\(y\)とする」ように式や関数で表現します。
\(B, C\):問題を絞り込む
漠然とした疑問(抽象的な課題)をより明確な課題に適応していきます。これを「問題を焦点化」といいます。そこから「どこまで解けばいいのか?」「具体的に何を求めれば解決になるのか?」をはっきりさせ、数学的にアプローチできる形にします。
\(C\):数学の手法を使って解決し、結果を得る
方程式を解く、図形の性質を使う、確率を計算する…など、その問題にあった数学的手法を用いて答えを導きます。結果としては答えそのものだけでなく、新たなアイデアや見通しが得られる場合もあります。
\(D_1\):解決結果を現実世界に戻して活用・意味づけをする
算出した答えや気づきが、日常生活や社会の文脈でどのように役に立つか、どのような意味を持つのかを再確認します。
必要に応じて計画を修正したり、新しい課題を発見したり、さらに発展させたりすることで、また次のステップ(ぐるぐる)につなげていきます。
図全体が「現実 → 数学 → 現実 → 数学」というサイクルを「ぐるぐる」と回っているように描かれているので、「ぐるぐるの図」と呼ばれています。これによって「算数・数学は世の中のさまざまなことを捉え、整理し、解決策を探るための強力な道具である」という考え方が伝わりやすくなるわけです。





